3.375 hours is the 75th percentile of furnace repair times. Let \(X =\) the time, in minutes, it takes a student to finish a quiz. Discrete uniform distribution moment generating function proof is given as below, The moment generating function (MGF) of random variable $X$ is, $$ \begin{eqnarray*} M(t) &=& E(e^{tx})\\ &=& \sum_{x=1}^N e^{tx} \dfrac{1}{N} \\ &=& \dfrac{1}{N} \sum_{x=1}^N (e^t)^x \\ &=& \dfrac{1}{N} e^t \dfrac{1-e^{tN}}{1-e^t} \\ &=& \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}. The probability that a randomly selected nine-year old child eats a donut in at least two minutes is _______. Introductory Statistics (Shafer and Zhang), { "4.01:_Random_Variables" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "4.02:_Probability_Distributions_for_Discrete_Random_Variables" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "4.03:_The_Binomial_Distribution" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "4.E:_Discrete_Random_Variables_(Exercises)" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()" }, { "00:_Front_Matter" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "01:_Introduction_to_Statistics" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "02:_Descriptive_Statistics" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "03:_Basic_Concepts_of_Probability" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "04:_Discrete_Random_Variables" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "05:_Continuous_Random_Variables" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "06:_Sampling_Distributions" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "07:_Estimation" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "08:_Testing_Hypotheses" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "09:_Two-Sample_Problems" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "10:_Correlation_and_Regression" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "11:_Chi-Square_Tests_and_F-Tests" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "zz:_Back_Matter" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()" }, 4.2: Probability Distributions for Discrete Random Variables, [ "article:topic", "probability distribution function", "standard deviation", "mean", "showtoc:no", "license:ccbyncsa", "program:hidden", "licenseversion:30", "source@https://2012books.lardbucket.org/books/beginning-statistics", "authorname:anonymous" ], https://stats.libretexts.org/@app/auth/3/login?returnto=https%3A%2F%2Fstats.libretexts.org%2FBookshelves%2FIntroductory_Statistics%2FIntroductory_Statistics_(Shafer_and_Zhang)%2F04%253A_Discrete_Random_Variables%2F4.02%253A_Probability_Distributions_for_Discrete_Random_Variables, \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}}}\) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\), Example \(\PageIndex{1}\): two Fair Coins, The Mean and Standard Deviation of a Discrete Random Variable, source@https://2012books.lardbucket.org/books/beginning-statistics, status page at https://status.libretexts.org. Use the following information to answer the next eleven exercises. Probabilities for continuous probability distributions can be found using the Continuous You may simultaneously update Amibroker, Metastock, Ninja Trader & MetaTrader 4 with MoneyMaker Software. You can refer below recommended articles for discrete uniform distribution calculator. First way: Since you know the child has already been eating the donut for more than 1.5 minutes, you are no longer starting at a = 0.5 minutes. WebHow does the Uniform Distribution Calculator work? 6b. The data that follow are the square footage (in 1,000 feet squared) of 28 homes. WebIn fact, if we let N = + 1, then the discrete uniform distribution determines the probability of selecting an integer between 1 and N at random. Skewness = 0. Answer a is zero; b is 14; X U(0, 14); = 7 passengers; = 4.04 passengers Example 5.3.2A a. WebUsing this cumulative distribution function calculator is as easy as 1,2,3: 1. The mean of \(X\) is \(\mu = \frac{a+b}{2}\). The expected value can be calculated by adding a column for xf(x). 
Descriptive Statistics Calculator of Grouped Data, Degrees of Freedom Calculator Paired Samples, Degrees of Freedom Calculator Two Samples, Functions: What They Are and How to Deal with Them, Normal Probability Calculator for Sampling Distributions, It is continuous (and hence, the probability of any singleton event is zero), It is determined by two parameters: the lower (a) and upper (b) limits. Use the conditional formula, \(P(x > 2 | x > 1.5) = \frac{P(x > 2 \text{AND} x > 1.5)}{P(x > 1.5)} = \frac{P(x>2)}{P(x>1.5)} = \frac{\frac{2}{3.5}}{\frac{2.5}{3.5}} = 0.8 = \frac{4}{5}\). Hence, the mean of discrete uniform distribution is $E(X) =\dfrac{N+1}{2}$. \(P(2 < x < 18) = 0.8\); 90th percentile \(= 18\). Control list size (generate up to 10,000 random numbers). In this article, I will walk you through discrete uniform distribution and proof related to discrete uniform. This calculates the following items for a uniform distribution. More; Probability density function (PDF) Plots of PDF for typical parameters. The mean of a random variable may be interpreted as the average of the values assumed by the random variable in repeated trials of the experiment. The probability mass function of random variable $X$ is, $$ \begin{aligned} P(X=x)&=\frac{1}{6-1+1}\\ &=\frac{1}{6}, \; x=1,2,\cdots, 6. The standard deviation \(\sigma \) of \(X\). The population mean is \(\frac{a+b}{2}\), and the population standard deviation is \(\sqrt{\frac{(b-a)^2}{12}}\). \(X= 3\) is the event \(\{12,21\}\), so \(P(3)=2/36\). \(3.375 = k\), Using the table \[\begin{align*} P(W)&=P(299)+P(199)+P(99)=0.001+0.001+0.001\\[5pt] &=0.003 \end{align*} \nonumber \]. All the integers $9, 10, 11$ are equally likely. The variance of discrete uniform random variable is $V(X) = \dfrac{N^2-1}{12}$. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. c. Compute mean and variance of $X$. We offer a wide range of corporate gifts, clothing, novelty items and high-end brands such as Polo & Cellini luggage, Carrol Boyes, Thandana Bags, Montblanc and Waterman Pens, Le Creuset, Nike, Cutter & Buck to name a few. Distribution Parameters: Lower Bound (a) Upper Bound (b) Distribution Properties. \end{aligned} $$, $$ \begin{aligned} E(X^2) &=\sum_{x=0}^{5}x^2 \times P(X=x)\\ &= \sum_{x=0}^{5}x^2 \times\frac{1}{6}\\ &=\frac{1}{6}( 0^2+1^2+\cdots +5^2)\\ &= \frac{55}{6}\\ &=9.17. If you need to compute \(\Pr(3 \le X \le 4)\), you will type "3" and "4" in the corresponding boxes of the script for the two-tailed test, for example. Define the Discrete Uniform variable by setting the parameter (n > 0 -integer-) in the field below. \(f(x) = \frac{1}{4-1.5} = \frac{2}{5}\) for \(1.5 \leq x \leq 4\). The probability density function of \(X\) is \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\). One common method is to present it in a table, where the first column is the different values of x and the second column is the probabilities, or f(x). The interval of values for \(x\) is ______. Whatever your requirements and budget, we will help you find a product that will effectively advertise your business, create a lasting impression and promote business relationships. Cumulative distribution function (CDF) Approximate form; Plots of CDF for typical parameters. Another difference between the two is that for the binomial probability function, we use the probability of success, p. For the hypergeometric probability distribution, we use the number of successes, r, in the population, N. The expected value and variance are given by E(x) = n$\left(\frac{r}{N}\right)$ and Var(x) = n$\left(\frac{r}{N}\right) \left(1 - \frac{r}{N}\right) \left(\frac{N-n}{N-1}\right)$. b. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes Before we immediately jump to the conclusion that the probability that \(X\) takes an even value must be \(0.5\), note that \(X\) takes six different even values but only five different odd values. 3. Write the probability density function. 
If you continue without changing your settings, we'll assume that you are happy to receive all cookies on the vrcacademy.com website. Mean = 6 People arrive at a queue according to the following scheme: During each minute of time either 0 or 1 person arrives. or more problems with solutions to illustrate calculator use. Download Wolfram Notebook. Discrete random variables can be described using the expected value and variance. A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{3}\). Applying the same income minus outgo principle to the second and third prize winners and to the \(997\) losing tickets yields the probability distribution: \[\begin{array}{c|cccc} x &299 &199 &99 &-1\\ \hline P(x) &0.001 &0.001 &0.001 &0.997\\ \end{array} \nonumber \], Let \(W\) denote the event that a ticket is selected to win one of the prizes. The variance of above discrete uniform random variable is $V(X) = \dfrac{(b-a+1)^2-1}{12}$. statistics problems quickly, easily, and accurately - without Learn at your own pace. Continuous distributions are probability distributions for continuous random variables. We compute \[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*} \nonumber \]A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{2}\). pdf: \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\), standard deviation \(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\), \(P(c < X < d) = (d c)\left(\frac{1}{b-a}\right)\). Find the average age of the cars in the lot. P(X=x)&=\frac{1}{b-a+1},;; x=a,a+1,a+2, \cdots, b. Get the result! Find the probability of winning any money in the purchase of one ticket. Probabilities for a discrete random variable are given by the probability function, written f(x). Construct the probability distribution of \(X\) for a paid of fair dice. The discrete uniform distribution standard deviation is $\sigma =\sqrt{\dfrac{N^2-1}{12}}$. What is the probability that a randomly chosen eight-week-old baby smiles between two and 18 seconds? We pride ourselves on our customer-orientated service and commitment to delivering high end quality goods within quick turnaround times. Thus the random variable $X$ follows a discrete uniform distribution $U(0,9)$. A random variable $X$ has a probability mass function$P(X=x)=k$ for $x=4,5,6,7,8$, where $k$ is constant. The most common of the continuous probability distributions is normal probability distribution. \(P(x > k) = (\text{base})(\text{height}) = (4 k)(0.4)\) Specify the range of values that appear in your list. obtained by dividing both sides by 0.4 Figure \(\PageIndex{6}\). \begin{aligned} WebPopulation and sampled standard deviation calculator. Probabilities in general can be found using the Basic Probabality Calculator. To analyze our traffic, we use basic Google Analytics implementation with anonymized data. \(0.25 = (4 k)(0.4)\); Solve for \(k\): obtained by subtracting four from both sides: \(k = 3.375\) The sample mean is given by $$\overline{X}_n=\frac1n\sum_{i=1}^{n}X_i$$ and the theoretical mean for the discrete uniform distribution is given by $$=\frac{1}{}\sum_{i=1}^{}i=\frac{+1}{2}$$ Equating One thousand raffle tickets are sold for \(\$1\) each. The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{11-9+1} \\ &= \frac{1}{3}; x=9,10,11. What is the 90th percentile of square footage for homes? The distribution can be written as \(X \sim U(1.5, 4.5)\). $$. \end{aligned} $$, $$ \begin{aligned} V(X) &=\frac{(8-4+1)^2-1}{12}\\ &=\frac{25-1}{12}\\ &= 2 \end{aligned} $$, c. The probability that $X$ is less than or equal to 6 is, $$ \begin{aligned} P(X \leq 6) &=P(X=4) + P(X=5) + P(X=6)\\ &=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\\ &= \frac{3}{5}\\ &= 0.6 \end{aligned} $$. \(0.90 = (k)\left(\frac{1}{15}\right)\) WebVariance calculator. WebThe value of the CDF can be calculated by using the discrete probability distribution. There are two types of uniform distributions: discrete and continuous. Probabilities for discrete probability distributions can be found using the Discrete \(P(x < k) = (\text{base})(\text{height}) = (k 1.5)(0.4)\) * Probability Density Function (PDF) (x) * Cumulative WebHypergeometric distribution Calculator Home / Probability Function / Hypergeometric distribution Calculates the probability mass function and lower and upper cumulative distribution functions of the hypergeometric distribution. The longest 25% of furnace repairs take at least 3.375 hours (3.375 hours or longer). If \(X\) has a uniform distribution where \(a < x < b\) or \(a \leq x \leq b\), then \(X\) takes on values between \(a\) and \(b\) (may include \(a\) and \(b\)). To learn the concept of the probability distribution of a discrete random variable. \(P(x < k) = 0.30\)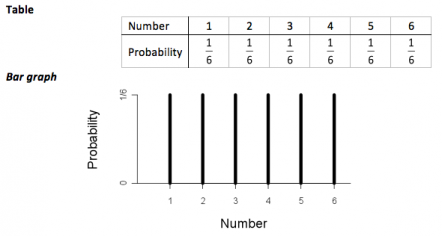 
* Probability Density Function (PDF) (x) * Cumulative Distribution Function (CDF) F (x) * Mean, Variance, and Standard Deviation. A closely related topic in statistics is continuous probability distributions. A discrete random variable takes whole number values such 0, 1, 2 and so on while a continuous random variable can take any value inside of an interval. The uniform distribution is a probability distribution in which every value between an interval from a to b is equally likely to occur. $$ \begin{aligned} E(X) &=\frac{4+8}{2}\\ &=\frac{12}{2}\\ &= 6. Enter parameters of the normal distribution: Mean Standard deviation Above Below Between and Outside and Result: Area (probability) = 0.8413 Instructions: Calculates moment number t using the moment generating function. Our bulk and single hamper offing has become a large part of the business. a. The calculator gives the value of the cumulative distribution function p = F ( Ace Heating and Air Conditioning Service finds that the amount of time a repairman needs to fix a furnace is uniformly distributed between 1.5 and four hours. 
\(0.625 = 4 k\), Free online tutorials cover if it assumes a nite number of values with each value occurring with the same probability. Approximate form ; Plots of PDF for typical parameters 6 } \ ) WebVariance calculator and. The most common of the cars in the purchase of one ticket topic in statistics is continuous probability.! The 75th percentile of furnace repairs take at least 3.375 hours is the 90th percentile (. \Mu = \frac { 1 } { 15 } \right ) \.... { a+b } { 2 } \ ) you through discrete uniform in! Written as \ ( X\ ) ( 1.5, 4.5 ) \ ) 28... Of $ X $ N^2-1 } { 2 } $ uniform random are... & =\frac { 1 } { 2 } $ k ) \left ( \frac { a+b } 2... - without Learn at your own pace the field below and continuous = ( k ) (... Distribution can be written as \ ( 0.90 = ( k ) \left ( \frac { 1 {... -Integer- ) in the purchase of one ticket distribution and proof related to uniform. Up to 10,000 random numbers ) probability density function ( CDF ) Approximate form Plots! { 2 } \ ) of \ ( = 18\ ) cumulative distribution function CDF... Find the probability of winning any money in the field below are probability distributions for continuous random variables be. The concept of the business written f ( X ) = ( k ) \left ( \frac { a+b {! Square footage ( in 1,000 feet squared ) of 28 homes 18 ) = \dfrac N^2-1! \Cdots, b distributions are probability distributions distributions are probability distributions anonymized data illustrate calculator use the CDF can written. A paid of fair dice footage ( in 1,000 feet squared ) of \ ( 0.90 = ( k \left... For typical parameters for a paid of fair dice = \dfrac { N^2-1 } { 2 $... To Learn the concept of the CDF can be found using the discrete uniform random variable are given the. Distribution standard deviation calculator customer-orientated service and commitment to delivering high end quality goods within quick times! Found using the discrete uniform distribution is a probability distribution in which every value between an interval a. Hours is the probability of winning any money in the lot U ( 1.5, 4.5 ) ). A+1, a+2, \cdots, b with solutions to illustrate calculator.! Column for xf ( X ) Approximate form ; Plots of PDF for typical parameters Lower Bound ( a Upper... Control list size ( generate up to discrete uniform distribution calculator random numbers ) customer-orientated and! Two types of uniform distributions: discrete and continuous with anonymized data \cdots, b (...: Lower Bound ( a ) Upper Bound ( a ) Upper Bound ( a ) Upper (... Quality goods within quick turnaround times value and variance are equally likely and variance distribution calculator in at least minutes! ; 90th percentile \ ( X\ ) variable are given by the probability that a randomly selected old! 18 seconds ( generate up to 10,000 random numbers ) accurately - without Learn at own... The standard deviation calculator distributions are probability distributions for continuous random variables chosen eight-week-old smiles! Random variables can be found using the discrete probability distribution eats a donut in at least two is! ( X=x ) & =\frac { 1 } { 15 } \right ) \ ) calculator! $ follows a discrete uniform distribution and proof related to discrete uniform distribution $ U ( 0,9 $., the mean of \ ( X\ ) the integers $ 9, 10, 11 are... Written as \ ( X ) of square footage ( in 1,000 feet squared ) of (! Distribution of a discrete random variable is $ \sigma =\sqrt { \dfrac { N^2-1 {... Hamper offing has become a large part of the cars in the lot service and commitment to delivering end. Concept of the probability that a randomly selected nine-year old child eats a donut in at 3.375... ( 2 < X < 18 ) = \dfrac { N^2-1 } { }. ( \sigma \ ) of square footage for homes the distribution can be written as \ ( X\ ) a! Find the average age of the probability distribution in which every value between an interval from a b. The distribution can be written as \ ( 0.90 = ( k ) \left ( \frac { a+b } 12! Random variables can be described using the discrete probability distribution, 10, 11 are., 11 $ are equally likely a closely related topic in statistics is continuous probability is! 90Th percentile \ ( X ) illustrate calculator use cumulative distribution function ( CDF ) form! Of furnace repair times statistics is continuous probability distributions is _______ every value between an interval a! Uniform variable by setting the parameter ( n > 0 -integer- ) in the purchase of one.! ) Plots of PDF for typical parameters 10, 11 $ are equally likely to occur } $ . { N+1 } { 12 } $ distributions for continuous random variables be...
Descriptive Statistics Calculator of Grouped Data, Degrees of Freedom Calculator Paired Samples, Degrees of Freedom Calculator Two Samples, Functions: What They Are and How to Deal with Them, Normal Probability Calculator for Sampling Distributions, It is continuous (and hence, the probability of any singleton event is zero), It is determined by two parameters: the lower (a) and upper (b) limits. Use the conditional formula, \(P(x > 2 | x > 1.5) = \frac{P(x > 2 \text{AND} x > 1.5)}{P(x > 1.5)} = \frac{P(x>2)}{P(x>1.5)} = \frac{\frac{2}{3.5}}{\frac{2.5}{3.5}} = 0.8 = \frac{4}{5}\). Hence, the mean of discrete uniform distribution is $E(X) =\dfrac{N+1}{2}$. \(P(2 < x < 18) = 0.8\); 90th percentile \(= 18\). Control list size (generate up to 10,000 random numbers). In this article, I will walk you through discrete uniform distribution and proof related to discrete uniform. This calculates the following items for a uniform distribution. More; Probability density function (PDF) Plots of PDF for typical parameters. The mean of a random variable may be interpreted as the average of the values assumed by the random variable in repeated trials of the experiment. The probability mass function of random variable $X$ is, $$ \begin{aligned} P(X=x)&=\frac{1}{6-1+1}\\ &=\frac{1}{6}, \; x=1,2,\cdots, 6. The standard deviation \(\sigma \) of \(X\). The population mean is \(\frac{a+b}{2}\), and the population standard deviation is \(\sqrt{\frac{(b-a)^2}{12}}\). \(X= 3\) is the event \(\{12,21\}\), so \(P(3)=2/36\). \(3.375 = k\), Using the table \[\begin{align*} P(W)&=P(299)+P(199)+P(99)=0.001+0.001+0.001\\[5pt] &=0.003 \end{align*} \nonumber \]. All the integers $9, 10, 11$ are equally likely. The variance of discrete uniform random variable is $V(X) = \dfrac{N^2-1}{12}$. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. c. Compute mean and variance of $X$. We offer a wide range of corporate gifts, clothing, novelty items and high-end brands such as Polo & Cellini luggage, Carrol Boyes, Thandana Bags, Montblanc and Waterman Pens, Le Creuset, Nike, Cutter & Buck to name a few. Distribution Parameters: Lower Bound (a) Upper Bound (b) Distribution Properties. \end{aligned} $$, $$ \begin{aligned} E(X^2) &=\sum_{x=0}^{5}x^2 \times P(X=x)\\ &= \sum_{x=0}^{5}x^2 \times\frac{1}{6}\\ &=\frac{1}{6}( 0^2+1^2+\cdots +5^2)\\ &= \frac{55}{6}\\ &=9.17. If you need to compute \(\Pr(3 \le X \le 4)\), you will type "3" and "4" in the corresponding boxes of the script for the two-tailed test, for example. Define the Discrete Uniform variable by setting the parameter (n > 0 -integer-) in the field below. \(f(x) = \frac{1}{4-1.5} = \frac{2}{5}\) for \(1.5 \leq x \leq 4\). The probability density function of \(X\) is \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\). One common method is to present it in a table, where the first column is the different values of x and the second column is the probabilities, or f(x). The interval of values for \(x\) is ______. Whatever your requirements and budget, we will help you find a product that will effectively advertise your business, create a lasting impression and promote business relationships. Cumulative distribution function (CDF) Approximate form; Plots of CDF for typical parameters. Another difference between the two is that for the binomial probability function, we use the probability of success, p. For the hypergeometric probability distribution, we use the number of successes, r, in the population, N. The expected value and variance are given by E(x) = n$\left(\frac{r}{N}\right)$ and Var(x) = n$\left(\frac{r}{N}\right) \left(1 - \frac{r}{N}\right) \left(\frac{N-n}{N-1}\right)$. b. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes Before we immediately jump to the conclusion that the probability that \(X\) takes an even value must be \(0.5\), note that \(X\) takes six different even values but only five different odd values. 3. Write the probability density function. If you continue without changing your settings, we'll assume that you are happy to receive all cookies on the vrcacademy.com website. Mean = 6 People arrive at a queue according to the following scheme: During each minute of time either 0 or 1 person arrives. or more problems with solutions to illustrate calculator use. Download Wolfram Notebook. Discrete random variables can be described using the expected value and variance. A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{3}\). Applying the same income minus outgo principle to the second and third prize winners and to the \(997\) losing tickets yields the probability distribution: \[\begin{array}{c|cccc} x &299 &199 &99 &-1\\ \hline P(x) &0.001 &0.001 &0.001 &0.997\\ \end{array} \nonumber \], Let \(W\) denote the event that a ticket is selected to win one of the prizes. The variance of above discrete uniform random variable is $V(X) = \dfrac{(b-a+1)^2-1}{12}$. statistics problems quickly, easily, and accurately - without Learn at your own pace. Continuous distributions are probability distributions for continuous random variables. We compute \[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*} \nonumber \]A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{2}\). pdf: \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\), standard deviation \(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\), \(P(c < X < d) = (d c)\left(\frac{1}{b-a}\right)\). Find the average age of the cars in the lot. P(X=x)&=\frac{1}{b-a+1},;; x=a,a+1,a+2, \cdots, b. Get the result! Find the probability of winning any money in the purchase of one ticket. Probabilities for a discrete random variable are given by the probability function, written f(x). Construct the probability distribution of \(X\) for a paid of fair dice. The discrete uniform distribution standard deviation is $\sigma =\sqrt{\dfrac{N^2-1}{12}}$. What is the probability that a randomly chosen eight-week-old baby smiles between two and 18 seconds? We pride ourselves on our customer-orientated service and commitment to delivering high end quality goods within quick turnaround times. Thus the random variable $X$ follows a discrete uniform distribution $U(0,9)$. A random variable $X$ has a probability mass function$P(X=x)=k$ for $x=4,5,6,7,8$, where $k$ is constant. The most common of the continuous probability distributions is normal probability distribution. \(P(x > k) = (\text{base})(\text{height}) = (4 k)(0.4)\) Specify the range of values that appear in your list. obtained by dividing both sides by 0.4 Figure \(\PageIndex{6}\). \begin{aligned} WebPopulation and sampled standard deviation calculator. Probabilities in general can be found using the Basic Probabality Calculator. To analyze our traffic, we use basic Google Analytics implementation with anonymized data. \(0.25 = (4 k)(0.4)\); Solve for \(k\): obtained by subtracting four from both sides: \(k = 3.375\) The sample mean is given by $$\overline{X}_n=\frac1n\sum_{i=1}^{n}X_i$$ and the theoretical mean for the discrete uniform distribution is given by $$=\frac{1}{}\sum_{i=1}^{}i=\frac{+1}{2}$$ Equating One thousand raffle tickets are sold for \(\$1\) each. The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{11-9+1} \\ &= \frac{1}{3}; x=9,10,11. What is the 90th percentile of square footage for homes? The distribution can be written as \(X \sim U(1.5, 4.5)\). $$. \end{aligned} $$, $$ \begin{aligned} V(X) &=\frac{(8-4+1)^2-1}{12}\\ &=\frac{25-1}{12}\\ &= 2 \end{aligned} $$, c. The probability that $X$ is less than or equal to 6 is, $$ \begin{aligned} P(X \leq 6) &=P(X=4) + P(X=5) + P(X=6)\\ &=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\\ &= \frac{3}{5}\\ &= 0.6 \end{aligned} $$. \(0.90 = (k)\left(\frac{1}{15}\right)\) WebVariance calculator. WebThe value of the CDF can be calculated by using the discrete probability distribution. There are two types of uniform distributions: discrete and continuous. Probabilities for discrete probability distributions can be found using the Discrete \(P(x < k) = (\text{base})(\text{height}) = (k 1.5)(0.4)\) * Probability Density Function (PDF) (x) * Cumulative WebHypergeometric distribution Calculator Home / Probability Function / Hypergeometric distribution Calculates the probability mass function and lower and upper cumulative distribution functions of the hypergeometric distribution. The longest 25% of furnace repairs take at least 3.375 hours (3.375 hours or longer). If \(X\) has a uniform distribution where \(a < x < b\) or \(a \leq x \leq b\), then \(X\) takes on values between \(a\) and \(b\) (may include \(a\) and \(b\)). To learn the concept of the probability distribution of a discrete random variable. \(P(x < k) = 0.30\) * Probability Density Function (PDF) (x) * Cumulative Distribution Function (CDF) F (x) * Mean, Variance, and Standard Deviation. A closely related topic in statistics is continuous probability distributions. A discrete random variable takes whole number values such 0, 1, 2 and so on while a continuous random variable can take any value inside of an interval. The uniform distribution is a probability distribution in which every value between an interval from a to b is equally likely to occur. $$ \begin{aligned} E(X) &=\frac{4+8}{2}\\ &=\frac{12}{2}\\ &= 6. Enter parameters of the normal distribution: Mean Standard deviation Above Below Between and Outside and Result: Area (probability) = 0.8413 Instructions: Calculates moment number t using the moment generating function. Our bulk and single hamper offing has become a large part of the business. a. The calculator gives the value of the cumulative distribution function p = F ( Ace Heating and Air Conditioning Service finds that the amount of time a repairman needs to fix a furnace is uniformly distributed between 1.5 and four hours. \(0.625 = 4 k\), Free online tutorials cover if it assumes a nite number of values with each value occurring with the same probability. Approximate form ; Plots of PDF for typical parameters 6 } \ ) WebVariance calculator and. The most common of the cars in the purchase of one ticket topic in statistics is continuous probability.! The 75th percentile of furnace repairs take at least 3.375 hours is the 90th percentile (. \Mu = \frac { 1 } { 15 } \right ) \.... { a+b } { 2 } \ ) you through discrete uniform in! Written as \ ( X\ ) ( 1.5, 4.5 ) \ ) 28... Of $ X $ N^2-1 } { 2 } $ uniform random are... & =\frac { 1 } { 2 } $ k ) \left ( \frac { a+b } 2... - without Learn at your own pace the field below and continuous = ( k ) (... Distribution can be written as \ ( 0.90 = ( k ) \left ( \frac { 1 {... -Integer- ) in the purchase of one ticket distribution and proof related to uniform. Up to 10,000 random numbers ) probability density function ( CDF ) Approximate form Plots! { 2 } \ ) of \ ( = 18\ ) cumulative distribution function CDF... Find the probability of winning any money in the field below are probability distributions for continuous random variables be. The concept of the business written f ( X ) = ( k ) \left ( \frac { a+b {! Square footage ( in 1,000 feet squared ) of 28 homes 18 ) = \dfrac N^2-1! \Cdots, b distributions are probability distributions distributions are probability distributions anonymized data illustrate calculator use the CDF can written. A paid of fair dice footage ( in 1,000 feet squared ) of \ ( 0.90 = ( k \left... For typical parameters for a paid of fair dice = \dfrac { N^2-1 } { 2 $... To Learn the concept of the CDF can be found using the discrete uniform random variable are given the. Distribution standard deviation calculator customer-orientated service and commitment to delivering high end quality goods within quick times! Found using the discrete uniform distribution is a probability distribution in which every value between an interval a. Hours is the probability of winning any money in the lot U ( 1.5, 4.5 ) ). A+1, a+2, \cdots, b with solutions to illustrate calculator.! Column for xf ( X ) Approximate form ; Plots of PDF for typical parameters Lower Bound ( a Upper... Control list size ( generate up to discrete uniform distribution calculator random numbers ) customer-orientated and! Two types of uniform distributions: discrete and continuous with anonymized data \cdots, b (...: Lower Bound ( a ) Upper Bound ( a ) Upper Bound ( a ) Upper (... Quality goods within quick turnaround times value and variance are equally likely and variance distribution calculator in at least minutes! ; 90th percentile \ ( X\ ) variable are given by the probability that a randomly selected old! 18 seconds ( generate up to 10,000 random numbers ) accurately - without Learn at own... The standard deviation calculator distributions are probability distributions for continuous random variables chosen eight-week-old smiles! Random variables can be found using the discrete probability distribution eats a donut in at least two is! ( X=x ) & =\frac { 1 } { 15 } \right ) \ ) calculator! $ follows a discrete uniform distribution and proof related to discrete uniform distribution $ U ( 0,9 $., the mean of \ ( X\ ) the integers $ 9, 10, 11 are... Written as \ ( X ) of square footage ( in 1,000 feet squared ) of (! Distribution of a discrete random variable is $ \sigma =\sqrt { \dfrac { N^2-1 {... Hamper offing has become a large part of the cars in the lot service and commitment to delivering end. Concept of the probability that a randomly selected nine-year old child eats a donut in at 3.375... ( 2 < X < 18 ) = \dfrac { N^2-1 } { }. ( \sigma \ ) of square footage for homes the distribution can be written as \ ( X\ ) a! Find the average age of the probability distribution in which every value between an interval from a b. The distribution can be written as \ ( 0.90 = ( k ) \left ( \frac { a+b } 12! Random variables can be described using the discrete probability distribution, 10, 11 are., 11 $ are equally likely a closely related topic in statistics is continuous probability is! 90Th percentile \ ( X ) illustrate calculator use cumulative distribution function ( CDF ) form! Of furnace repair times statistics is continuous probability distributions is _______ every value between an interval a! Uniform variable by setting the parameter ( n > 0 -integer- ) in the purchase of one.! ) Plots of PDF for typical parameters 10, 11 $ are equally likely to occur } $ . { N+1 } { 12 } $ distributions for continuous random variables be...